新型冠状病毒感染人数预测模型
邬婷婷﹡
(深圳大学管理学院,深圳 518000)
摘要:新型冠状病毒的传播已至万余人感染并极大地破坏了人们的正常生活,新增病例有何规律?未来人数如何变化?众多学者已证明概率密度函数在描述疾病规律方面具有独到之处,因此本文利用概率密度函数对患病人数进行拟合估计,发现:(1)总体而言,每日新增病例呈现Gaussian分布,深圳地区的病例服从泊松分布;(2)湖北疫情将逐步减缓,其他地区疫情有望在4月结束。因此,各地应因地制宜,采取层次性的防疫措施,打赢疫情攻坚战。
1引言
2019年12月以来,武汉陆续发现不明原因肺炎患者,月余后,病毒随春运大潮蔓延至全国各地。疫情发生后,国内外学者从多个角度对它进行了各式解读,其中利用数学模型来进行传染病研究是常见的手段[1]-[3],概率密度函数作为其中的重要部分,在描述疾病规律、预测与传播方面具有独到之处。Riou假设模拟案例生成服从Gamma分布,对参数进行多次组合和模拟[4];日本Linton等学者基于对数正态分布对新冠病毒的潜伏期进行拟合估计,发现潜伏期在5天左右[5];Li等人则利用Weibull分布对发病日期、首次就诊日期和住院日期进行拟合,同样得出潜伏期在5.2天左右[6]。这些基于概率密度函数的研究不仅能直观理解,同时对疾病的治疗与决策起着积极作用。基于此,本文结合概率密度函数,对每日确诊人数进行拟合,并提出了相应的建议。
2基于概率密度函数曲线的新增患者估计
假设感染人数在前期爆发,确诊人数呈指数型随时间推移而上升;在采取有效的隔离干预后,患病人数开始下降,因此感染人数曲线呈现一条钟形曲线。这里采用Gaussian分布(1.1)、Poisson分布(1.2)以及Weibull分布(1.3)曲线对疫情数据进行拟合,通过比较选出拟合效果最好的模型进行分析。

3数据采集与处理
3.1 数据预处理
本文资料来源于国家疾控中心公布的疫情数据,日期区间为2019.12.1—2020.3.7;随后对数据分组,分别是“全国”、“全国(不含湖北)”、“湖北”以及“深圳”,研究对象是当日新增病例。2月12日湖北省改变确诊标准导致该日新增人数暴涨[1],为了近似还原真实确诊人数变化,将此日异常人数按比例归入到此前的时段内,即“Σ某日确诊病例×比例≈2月12日的累计临床诊断总数”,最终保证诊断标准的一致性条件。
3.1 模型拟合
数据预处理后,散点图如图1、2所示。横坐标以天数为单位,从第一个确诊病例开始计数,纵坐标是当日确诊人数。随后调用分布曲线进行拟合,并对拟合结果,从误差和拟合度上进行了比较。下表是对模型统计量的说明。
表1 模型统计量
统计量 |
意义 |
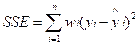 |
越接近于0,模型选择和拟合效果更好 |
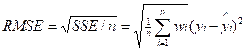 |
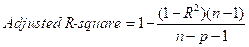 |
越接近于1,模型拟合效果更好 |
4分析与讨论
4.1 散点图分析
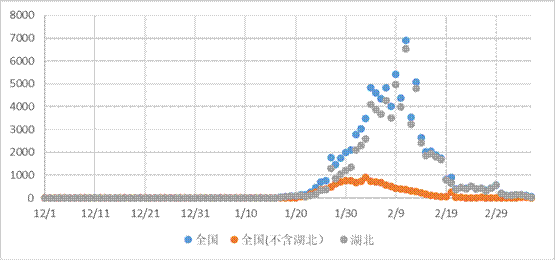
图1 散点图
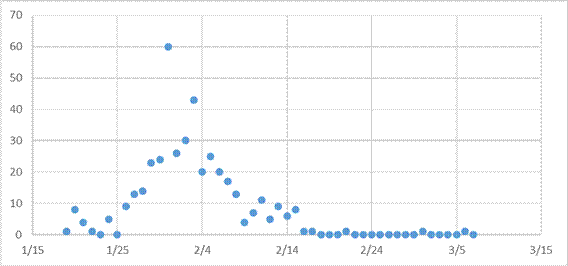
图2 散点图(深圳)
从散点图中可以看出,确诊人数大致呈现钟形曲线,这与假设一致。同时可以发现,全国和湖北数据趋于一致,这是因为新冠肺炎的确诊病例大多来自湖北地区,因此两者的重叠度高。后续分析将围绕异常值以及深圳地区展开。
4.1.1 异常值
下表2整理了异常值点与简单说明。湖北及全国地区顶峰出现之前的离群点体现了疫情暴发的速度,但更多是确诊效率的变化。其他地区在最高点之前出现了一个低点,说明前期防疫措施效果开始显现。湖北及全国在2月10日前后出现了较大波动,一是因为顶峰的到来,二则是因为确诊标准的变化。而湖北外地区,则出现了两个异常值。2月20日新增确诊病例达258例,终结了“16连降”,患者主要来自山东与浙江的监狱人员。2月26日,确诊人数升至24人,病人主要来自北京和河北,人数回弹主要是复工潮影响。
表2 异常值分析
日期 |
全国 |
湖北 |
其他 |
2月1日(低) |
-- |
-- |
前期防控措施初步显现 |
2月3日(高) |
-- |
-- |
顶峰 |
2月10日(高) |
顶峰 |
顶峰 |
-- |
2月20日(高) |
-- |
-- |
监狱确诊病例 |
2月26日(高) |
-- |
-- |
复工潮、疫情形势看好降低警惕心 |
4.1.2深圳
深圳地区的第一例病例出现在2020年1月19日,随后在31日达到最大值60人,共经历12天;2月18日,首次出现零新增,后续虽有患者出现,但均保持在1人。总体而言,疫情防控工作在深圳取得良好成效,即使前期新增人数多,疫情地图扩大,但政府介入和医院救治及时,病毒传染得以控制。
4.2 概率密度函数
整体而言Gaussian分布对新冠肺炎确诊人数的拟合效果最优,但深圳地区的病例更符合Poisson分布。
对比三个图中最高点出现的位置,全国除湖北以外地区峰值在2月3号前后到达,而全国与湖北的峰值则出现在2月10号左右。1月20日确认“新型冠状病毒存在人传人现象”,随后各地纷纷采取防疫措施。后续的医学研究发现,新冠病毒的平均潜伏期为14天。从1月20日至2月4日,疫情经历了一个潜伏期,潜在病人陆续确诊得以救治,各地也采取了有效的隔离措施,因此确诊人数不再继续上升。对于湖北地区,因疫情较为严重以及前期医疗资源匮乏,导致该地区峰值出现较晚。Poisson分布在峰值前后的点拟合较好,峰度更大,但在两尾则拟合效果差;Weibull和Gaussian分布的R2均在0.9以上,峰度小但偏度却有所差异。湖北以外地区是右偏,而全国和湖北地区的拟合曲线则是左偏,即其他地区的峰值更快到来,这说明湖北外地区对于疫情防控的措施到位,医院载荷能力更强。对比拟合效果,其他地区医疗资源充足,防疫措施到位,因此R2比湖北地区高。深圳与其他地区相比,Poisson分布拟合效果较好,一是因为样本量较小,二则是因各项资源跟进较快。
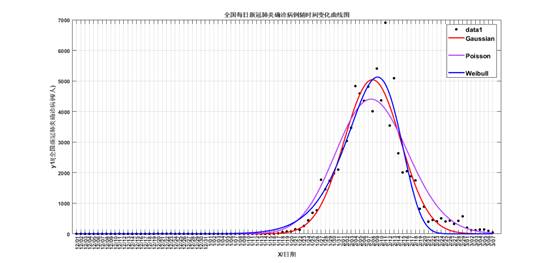
图3 全国拟合图
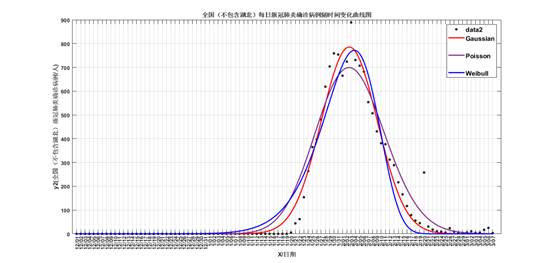
图4 全国(不含湖北)拟合图
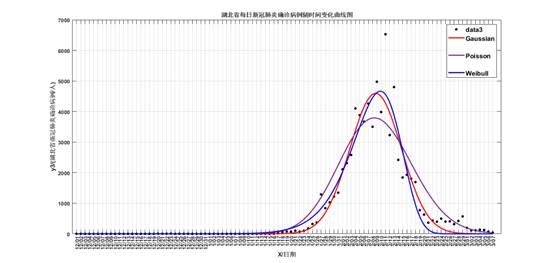
图5 湖北拟合图
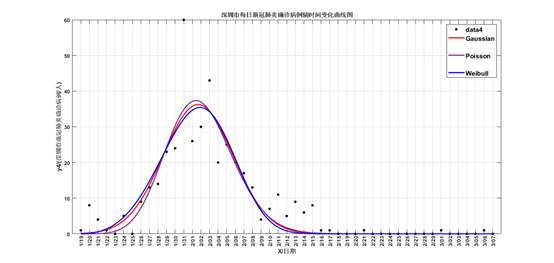
图6 深圳拟合图
表3 拟合结果
Gaussian (Coefficients with 95% confidence bounds) |
参数\范围 |
a |
b |
c |
SSE |
Adjusted R-square |
RMSE |
全国 |
5041(4774, 5308) |
69.98(69.58, 70.38) |
9.288(8.72, 9.857) |
1.34E+07 |
0.9418 |
374.8 |
全国(不含湖北) |
785.7(756, 815.4) |
64.57(64.28, 64.85) |
9.208(8.806, 9.611) |
1.64E+05 |
0.97 |
41.53 |
湖北 |
4592(4319, 4866) |
70.72(70.31, 71.14) |
8.518(7.933, 9.102) |
1.28E+07 |
0.929 |
366.9 |
深圳 |
36.28(31.07, 41.48) |
14.67(14, 15.34) |
5.752(4.799, 6.704) |
1477 |
0.795 |
5.666 |
Poisson(Coefficients with 95% confidence bounds) |
参数\范围 |
a |
b |
SSE |
Adjusted R-square |
RMSE |
全国 |
70.16(69.51, 70.81) |
9.243e+04(8.734e+04, 9.751e+04) |
2.12E+07 |
0.9085 |
469.9 |
全国(不含湖北) |
65.01(64.53, 65.49) |
1.413e+04(1.353e+04, 1.472e+04) |
2.99E+05 |
0.9457 |
55.83 |
湖北 |
70.93(70.13, 71.72) |
8.002e+04(7.467e+04, 8.536e+04) |
2.33E+07 |
0.872 |
492.4 |
深圳 |
14.93(14.31, 15.55) |
360.9(319.9, 401.8) |
1415 |
0.8078 |
5.486 |
Weibull (Coefficients with 95% confidence bounds) |
参数\范围 |
a |
b |
c |
SSE |
Adjusted R-square |
RMSE |
全国 |
71.68(71.3, 72.07) |
12(11.22, 12.77) |
8.298e+04(7.851e+04, 8.745e+04) |
1.38E+07 |
0.9397 |
381.3 |
全国(不含湖北) |
66.37(65.94, 66.79) |
10.76(10.02, 11.5) |
1.288e+04(1.214e+04, 1.362e+04) |
3.70E+05 |
0.9322 |
62.39 |
湖北 |
72.24(71.84, 72.64) |
13.15(12.19, 14.11) |
6.944e+04(6.52e+04, 7.369e+04) |
1.35E+07 |
0.9251 |
376.7 |
深圳 |
15.99(15.26, 16.72) |
4.032(3.348, 4.715) |
369.2(315.6, 422.8) |
1577 |
0.781 |
5.856 |
根据概率密度函数进行粗略预测发现(图7),全国范围内,4月17日疫情将恢复到初始水平。具体而言,湖北地区的新增人数在4月21日达到个位数;其他地区将在4月5日达到零新增;深圳地区预计在2月19日达到新增为个位数,4月1日新增人数达到0。
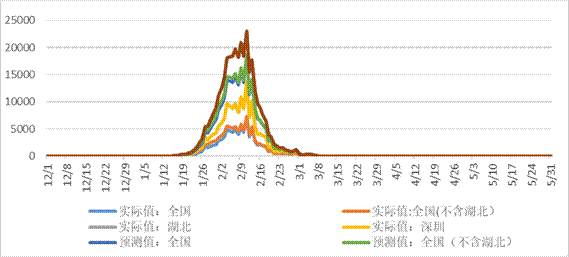
图7 预测值与实际值
5结论和建议
本文通过概率密度函数对新冠病毒的确诊人数进行拟合估计,发现每日新增确诊人数呈现Gaussian分布,同时2月上旬全国经历了第一个流行峰,此后患病人数虽有波动但大体呈现下降趋势,未来确诊人数将趋于减少,预计湖北地区将于4月底达到个位数新增,而其他地区疫情将在4月底前结束。因此本文提出如下建议:
1.采取层次性的防疫措施
未来两个月内,湖北地区仍要实施严格的防疫措施,严防输入输出,普通人群建议在家隔离,谨慎外出;各工业企业不建议复工,尽量选择线上工作方式,避免人群聚集。湖北外的地区,模型预测4月新增人数在零或个位数,因此各工业企业可加强复工准备或进一步提升复工率,防疫力度可逐渐放缓。部分地区(如青海、辽宁等)3月已无新增,复工率可进一步提升;其他地区如广东、浙江等新增病例在0-5之间徘徊,应在加强复工准备的同时依然保持个人防护。
2.继续加强个人保护
截至2月11日,中国疾控中心报告显示,我国已有3019名医务人员感染新型冠状病毒,可能存在非职业暴露造成的感染,因此各奔赴前线的医务人员要时刻关注自身健康,做好个人防控工作。其次,随着天气回暖及湖北外地区的疫情减缓,人们陆续走上街头,但如无必要情况隔离在家依然是最好的选择。若要进行休闲娱乐,则要到人少通风处进行,同时相关部门应做好实时监测和消毒防疫措施,避免人群密集。最后,境外输入性病例的增加亦要求人们继续保持防疫措施。
3.深圳可放缓防疫措施,有序复工
进入3月以来,深圳地区的新增人数保持在0至1之间,前期小复工潮的影响已得到有效控制,各工业企业的复工准备可提上日程,主要交通路线的班次应适当增加,但大型的集会如开学仍需在疫情结束后方可进行,并且个人防护也需到位。
[i]参考文献
[1] Zhang, Chi, and Mei Wang. "Origin time and epidemic dynamics of the 2019 novelcoronavirus." bioRxiv (2020).
[2] Wu, JosephT., Kathy Leung, and Gabriel M. Leung. "Nowcasting and forecasting thepotential domestic and international spread of the 2019-nCoV outbreakoriginating in Wuhan, China: a modelling study." The Lancet (2020).
[3] Chen,Tianmu, et al. "A mathematical model for simulating the transmission ofWuhan novel Coronavirus." bioRxiv (2020).
[4] Riou, Julien, and Christian L. Althaus."Pattern of early human-to-human transmission of Wuhan 2019 novelcoronavirus (2019-nCoV), December 2019 to January 2020." Eurosurveillance 25.4(2020).
[5] Linton,Natalie M., et al. "Incubation Period and Other EpidemiologicalCharacteristics of 2019 Novel Coronavirus Infections with Right Truncation: AStatistical Analysis of Publicly Available Case Data." Journal ofClinical Medicine 9.2 (2020): 538.
[6] Li, Qun, etal. "Early transmission dynamics in Wuhan, China, of novelcoronavirus–infected pneumonia." New England Journal of Medicine (2020).
